用细观力学模型估算镁碳耐火材料基质的力学性能
- 发布人:管理员
- 发布时间:2014-01-16
- 浏览量:4532
王志刚1,2) 李楠2) 孔建益1) 李友荣1)
1)武汉科技大学机械传动与制造工程湖北省重点实验室 武汉430081
2)武汉科技大学耐火材料与高温陶瓷省部共建国家重点实验室培育基地
摘要 利用细观力学模型,估算了树脂结合和沥青结合两种镁碳砖中基质的力学性能,并从其显微结构和组 成两方面探讨了其性能差异的原因。该方法为评估耐火材料基质的力学性能提供了一种新的思路。
关键词 细观力学,广义自洽模型,性能预测,镁碳质耐火材料
通常,耐火材料由骨料和基质两部分构成。基质 的结构和性质对耐火材料的整体性能有时起着决定 性的作用。如何评估耐火材料基质的性质是耐火材 料科技工作者关注的问题。将基质按组成制成单独 的试样进行研究是其中的一种方法,这种方法虽然可 以系统地研究基质组成结构及其性质,但有两个缺 点:一是费时、费力;二是并不能准确反映与骨料共存 的实际情况下基质的性质。
细观力学是目前研究复合材料显微结构与性质 的一种很有发展前景的方法。它是采用连续介质力 学和材料科学的一些理论,对材料的显微结构(微孔、 微裂纹、两相界面)进行力学描述的一种方法。它从 材料显微结构出发,利用弹性力学理论,建立材料组 成成分的局部性能、体积分数及其空间分布与材料宏 观有效性能的定量关系,揭示材料的显微结构与宏观 性能之间的内在关系。笔者曾利用细观力学方法研 究了Al2O3-C耐火材料的显微结构与性质的关系, 取得了较满意的效果[1]。
MgO-C质耐火材料是由镁砂骨料与基质构成 的复合材料,其基质由石墨、镁砂细粉、各种添加剂及 不同的结合剂构成。基质的组成与结构对耐火材料 的性质有很大影响。反过来,也可以根据耐火材料的 整体性质来估算基质的性质。本工作利用细观力学 模型,根据已有MgO-C砖的力学性能,对不同MgO -C质耐火材料中的碳基质相的力学性能进行了估 算,探讨用细观力学理论研究耐火材料显微结构与性 能关系的方法。
1 耐火材料的细观力学模型
根据复合材料显微结构的空间分布,可利用相应 的细观力学模型进行性能预测。耐火材料是典型的颗粒弥散多相复合材料。广义自洽模型(GSCS)是最 适合进行该类复合材料性能预测的方法[2]。
广义自洽模型(图1)的原理是将夹杂及其包围 的介质嵌入性能未知的无限大的等效均匀介质中,在 其边界施加相应的边界条件,通过应力场的求解获得复合材料的等效性能[3-4]。
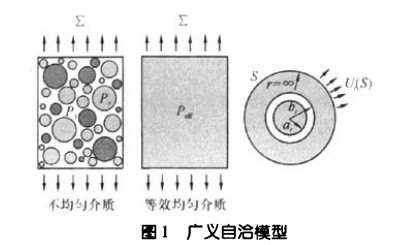
考虑一种非均质材料,它由N种各向同性成分组 成,各相的体积模量为墨,剪切模量为Gr(图l中P1 为基质相的性能,Pr为颗粒相的性能,Peff为等效均匀 介质的性能)。r等于1时对应连续相,r=2,3,L,N时 对应不同的颗粒相。耐火材料为夹杂弥散复合材料, 其微观结构由任意分布的复合球组装而成,因此,复 合材料的等效体积模量Keff、等效剪切模量Geff仍保持 各向同性。
等效刚度可通过在外边界(r→∞)施加均匀边界条件:
![]()
计算得到。此处,Ui为位移场,S为复合材料骨料的外边界, ![]() 为约束应变张量,xj为直角坐标系统。应变张量是球张量
为约束应变张量,xj为直角坐标系统。应变张量是球张量![]() 或偏张量
或偏张量![]() 为 Kroneckerδ。
为 Kroneckerδ。

由于材料的4个弹性常数(体积模量K、剪切模量 G、弹性模量E、泊松比ν)中只有2个独立量,可根据 (3a)、(3b)、(3c)式从K、G、E、ν中任意两个弹性常数 确定出其他2个弹性常数。由求得的体积模量K和剪 切模量G,利用弹性模量E,泊松比ν和Ltme系数λ之 间的关系(式3),可计算出材料的弹性性能。
![]()
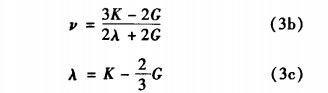
111 当复合材料为两相时,等效弹性性能可以由下面 的解析式确定。下列式中,K为体积模量、G为剪切 模量、E为弹性模量、ν为泊松比,C为体积分数,下标 i表示颗粒(骨料)相,m表示基质相,eff表示均质化 后材料的等效性能。
等效体积弹性模量可以表示为:
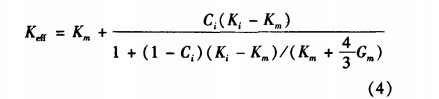
等效剪切模量满足以下方程:
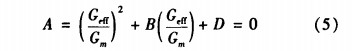
其中,方程的系数A、B、D由下式决定:
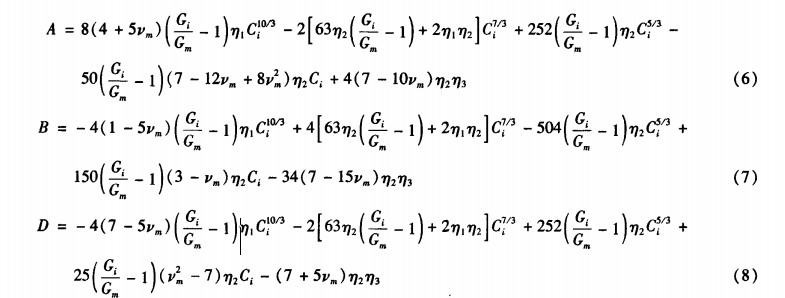
系数A、B、D中的η1,η,η3由下列式子确定:
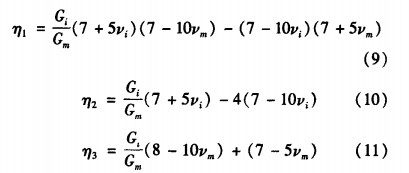
可见,对于两相复合材料,在骨料、基质和等效材 料三者之中已知其中两个的材料性能,则可以利用广 义自洽模型计算出另一个材料的性能。
2 耐火材料细观力学模型的应用
把镁碳质耐火材料看成在基质相中嵌入的不同 尺寸的镁砂骨料所组成的复合材料。其力学性能在很大程度上取决于这些相的内在性能、体积分数以及 它们的空间分布。
选择A、B两种镁碳砖为研究对象[5],其中,A为 树脂结合的,B为沥青结合的。它们的组成及力学性能列于表1中。
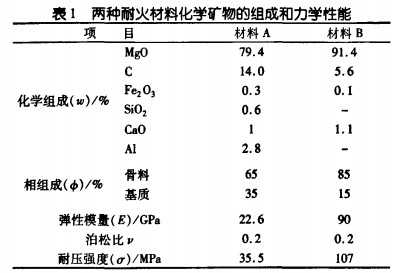
从表1中可以看出,两种耐火材料的弹性模量和 耐压强度有很大的差异。材料A的弹性模量和耐压 强度比材料B的低很多。
从力学观点看,这两种非均质材料都由两种相组 成:镁砂骨料可看作是一种不连续相;连续相包括碳结 合剂、片状石墨、镁砂细颗粒和附加的金属元素。两种 材料的气孔率都很小,可以忽略不计。因此,这两种耐 火材料都可以看作是由MgO颗粒相和基质相构成的 两相复合材料,可以直接利用GSCS模型建立颗粒相、 基质相和复合材料三者机械性能的定量关系。
图2为利用广义自洽模型对两相复合材料基质 相弹性性能进行预测的计算过程。
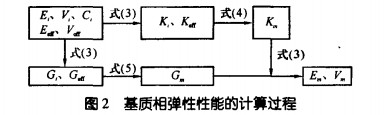
MgO-C质耐火材料中,MgO的弹性模量为248 GPa,泊松比为0.23。利用图2所示的计算过程,根 据两种材料的力学性能指标及两种材料中各相的体 积分数,可以计算出两种不同耐火材料中基质的性 能。表2列出了两种不同耐火材料中基质性能的计 算值。由表2中可以看出这两种材料基质的机械性 能有较大差异。这种差异可能来自于它们组成和结 构的不同。

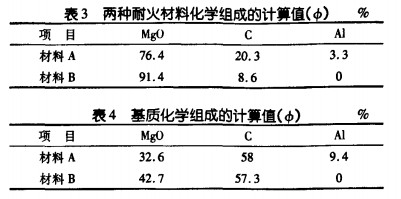
根据表1列出的化学组成,将各成分的质量分数 转换成体积分数,并认为Fe2O3、SiO2及CaO为镁砂 带来的杂质,记人MgO的体积分数中。取MgO的体 积密度为3.4 g·cm-3,C的体积密度为2.2 g·cm-3,Al的体积密度为2.7 g·cm-3,根据体积与 质量的关系,计算出两种材料按体积分数的化学组成 (见表3)。对照表3中计算出的Mgo的体积分数和 表l中骨料的体积分数可以发现,MgO的体积分数比 骨料相的体积分数大,认为这部分差值对应的Mgo 全部进入到基质相中。这样,可以计算出两种材料基 质相的化学组成(见表4)。从表4中可以看到两种 材料基质组成的差异。材料A的基质中MgO与C的 体积比为l:1.78,材料B的基质中MgO与C的体积 比为1:1.34。显然,材料B的基质中MgO的含量高。这是造成材料B的基质弹性模量高的原因之一。
另外,不同结合剂炭化后显微结构不同也是可能 的原因之一。树脂结合剂的残炭结构是玻璃状的非 石墨化的炭,密度比沥青结合剂的小,而沥青结合剂 的残炭结构是由具有石墨特性的稳定的不规则非晶 相组成[6],因此,沥青结合剂炭化后形成的C相的弹 性模量应该比树脂结合剂的大。此外,在材料A中有 Al存在也可能是其弹性模量低的另一原因。
因此,基质中镁砂与碳含量比例以及碳的显微结 构的差异,添加剂的存在都可能造成基质性能的差异。
3 结论
利用细观力学的方法,对不同镁碳质耐火材料中 基质相的弹性性能进行了估算,得出了一些有意义的 结果,为细观力学方法在耐火材料中的应用进行了前 期探索,并证明细观力学在研究耐火材料显微结构和 性能关系方面是一种新的有效方法。

【中国镁质材料网 采编:ZY





